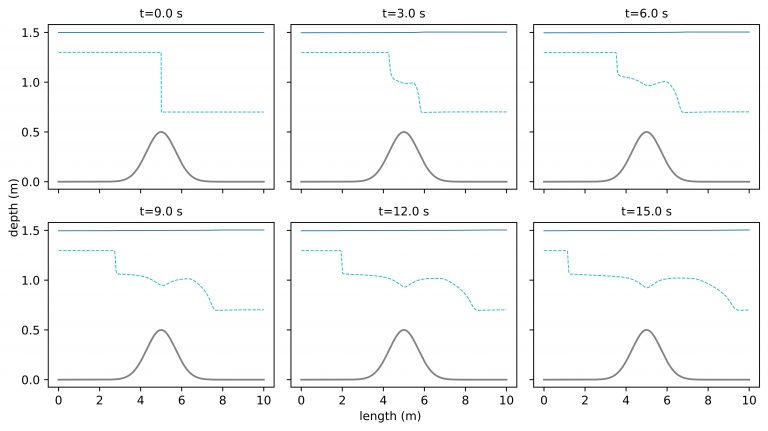
The efficiency of several first-order numerical schemes for two-layer shallow water equations (SWE) are evaluated here by considering different eigenvalue solutions. This study is a continuation of our previous work (Krvavica et al., 2018) in which we have proposed an efficient implementation of a Roe solver for two-layer SWE based on analytical expressions for eigenvalues and eigenvectors. In this work, the accuracy and computational cost of numerical, analytical, and approximated eigenvalue solvers are compared when implemented in Roe, Intermediate Field CaPturing (IFCP) and Polynomial Viscosity Matrix (PVM) schemes. Several numerical tests are performed to examine the overall efficiency of numerical schemes with different eigenvalue solvers when computing two-layer shallow-water flows. The results confirm that analytical eigenvalue solutions are much faster than numerical solvers, with a computational cost closer to approximate expressions. Consequently, the Roe scheme with analytical solutions to the eigenstructure is equally efficient as the IFCP scheme. On the other hand, IFCP and PVM schemes with analytical solutions to eigenvalues are found to be equally efficient as those with approximated expressions. Analytical eigenvalues show slightly better results when dealing with larger density differences between the layers.