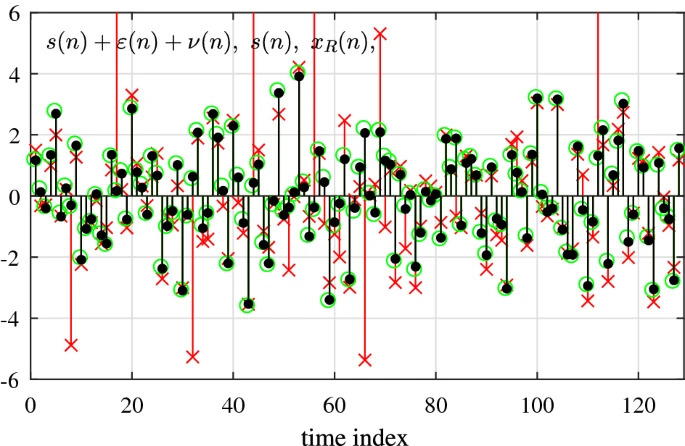
In this paper, we present an approach to the reconstruction of signals exhibiting sparsity in a transformation domain, having some heavily disturbed samples. This sparsity-driven signal recovery exploits a carefully suited random sampling consensus (RANSAC) methodology for the selection of a subset of inlier samples. To this aim, two fundamental properties are used: A signal sample represents a linear combination of the sparse coefficients, whereas the disturbance degrades the original signal sparsity. The properly selected samples are further used as measurements in the sparse signal reconstruction, performed using algorithms from the compressive sensing framework. Besides the fact that the disturbance degrades signal sparsity in the transformation domain, no other disturbance-related assumptions are made—there are no special requirements regarding its statistical behavior or the range of its values. As a case study, the discrete Fourier transform is considered as a domain of signal sparsity, owing to its significance in signal processing theory and applications. Numerical results strongly support the presented theory. In addition, the exact relation for the signal-to-noise ratio of the reconstructed signal is also presented. This simple result, which conveniently characterizes the RANSAC-based reconstruction performance, is numerically confirmed by a set of statistical examples.